프로젝트 설명
총 2개의 글을 통해 최소자승법의 이해와 이용 방법에 대해 정리해보려고 한다.
우선 이 글에서는 최소자승법이 무엇인지, 어떻게 쓰이는지, 그리고 선형 최소자승 문제를 어떻게 푸는지에 대해 알아보고
두 번째 글을 통해서는 비선형 최소자승 문제에 접근하는 방법에 대해 다뤄보려고 한다.
우선 이 프로젝트는, 원을 표현하는 n개의 (x, y) 좌표들이 주어졌을 때, 이 데이터들과 오차가 제일 적은 최적의 원을 찾고 싶어서 시작하게 되었다. 회사의 모든 분들이 최소자승법이 무엇인지 알고 지금껏 다항식 피팅 범용 함수를 이용해 왔지만, 범용 함수의 원리를 이해하시거나 최소자승법의 다양한 계산 방법을 알고 활용하시는 분은 없었기 때문에, 최소자승법을 통해 최적의 원을 찾는 방법을 조사하는 겸사겸사 최소자승법에 대해 공부하고 발표하게 되었다. 내가 적어나갈 3개의 글들 또한 최적의 원을 찾는데에 국한되지 않고, 최소자승법이라는 큰 그림을 이해하는 데에 목적을 둔다.
Least Square Method (최소자승법)
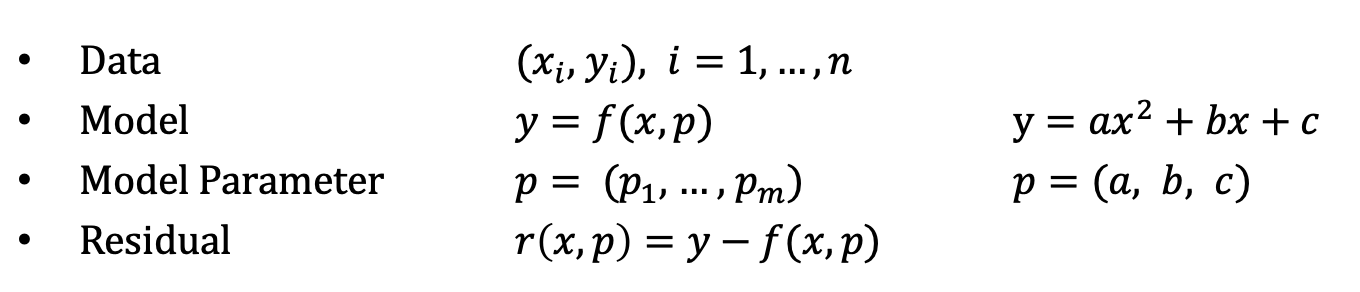
먼저 우리는 데이터, 즉 n개의 즉 관측값이 있고, 이 관측값들이 보이는 경향성을 통해 함수 모델을 정한다.
최소자승법은 관측 값과 우리가 정한 모델 사이의 residual (오차)의 제곱의 합이 최소가 되도록, 모델 파라미터를 정하는 것이다.
즉, 위의 4가지 정보에서 변수는 오직 모델 파라미터 하나, m개의 변수라고 볼 수 있다.
최소자승문제는 모델 파라미터에 대해 선형이냐 비선형이냐로 접근법이 크게 달라진다.
우리가 일반적으로 이야기하는 최소자승법은 모델 파라미터에 대해 선형인 문제를 푸는 방법인데, 이는 closed-form solution을 통해 최적의 모델 파라미터를 구할 수 있다. 반면에, 모델 파라미터에 대해 비선형인 경우에는 closed-form solution이 존재하지 않기 때문에, residual = 0인 방정식의 근사해를 찾는 방법이나, 방정식의 최솟값을 찾는 방법으로 접근해야 한다.
앞서 말했듯이 이 글에서는 선형일 경우에 대해서만 이야기해 보겠다.
Linear Least Squares (선형 최소자승 문제)
: closed-form solution O
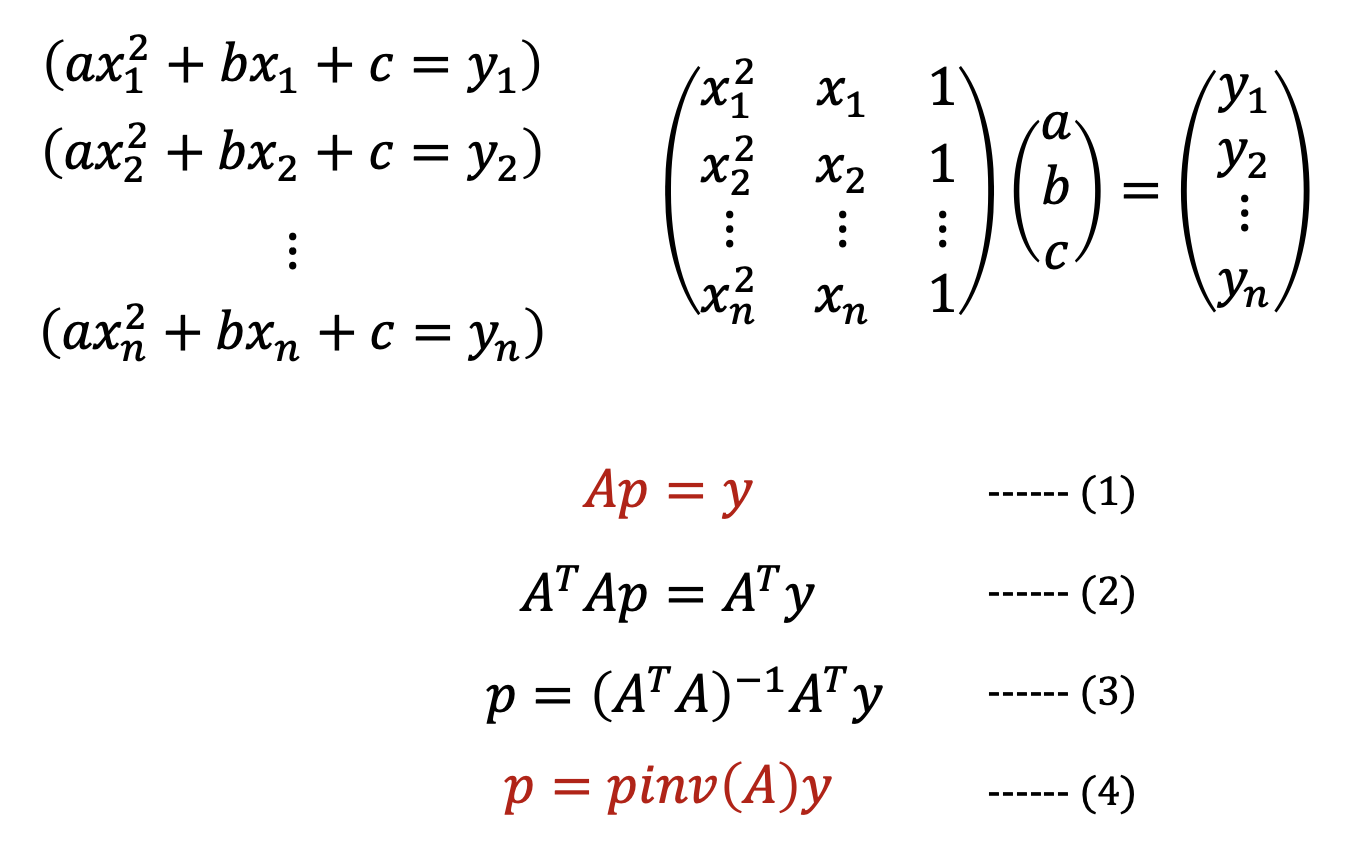
n개의 (x, y) 데이터가 있고, 우리는 이 데이터가 2차 함수를 따르는 것 같다고 생각한다고 가정해보자.
이때, "어떤 2차 함수를 따를까?" 라는 질문에 대답하기 위한 하나의 접근법이 최소자승법인 것이다.
즉, 최소자승법은, 우리가 가지고 있는 데이터 값과 함숫값의 차이의 제곱이 최소가 되는 2차 함수의 계수 p = (a, b, c)를 구하자는 것이다.
데이터와 모델 함수를 아는 이상 우리는 상단 좌측과 같이 n개의 식을 만들어낼 수 있고
이 n개의 식은 상단 우측과 같은 행렬식으로, 수식 (1)과 같이 표현할 수 있다.
closed-form solution이 존재한다는 말은, p의 값이 정해져 있다는 소리이다.
(1)로부터 계산의 편리를 위해 양변에 A의 전치행렬을 곱해주면 (2)가 되고
p를 제외한 모든 것을 우변으로 넘기면 (3)번 식이, 곧 (4)번 수식이 나온다.
결론적으로 우리가 구하고자 하는 p는 (4)와 같다. 이것이 증명된 우리의 최소제곱해인 것이다.
이 Closed-form Solution의 의미
궁금했다. 저게 답이라는 걸 어떻게 알지?
n이 구하고자 하는 계수의 수보다 (변수의 개수보다) 크다면, 위의 Ap = y라는 연립방정식 해는 어떻게 구해지는 거지?
아래에서 두 가지 방법으로 간단하게나마 이해를 도와보겠다.
기하학적 의미
그림이 p와 y 대신 각각 x와 b를 사용하니 여기에서부터 Ax = b로 이야기를 해보자.
우리의 목적은 Ax = b를 제일 근사하게 만족시키는 x(모델 파라미터 벡터)를 찾는 것이다.
즉, Ax와 b 사이의 거리가 최소가 되는 x를 최소제곱해 (least squares solution)라고 부르고, 찾는 것이다.
언제 Ax와 b의 차이가 최소가 될까? 그림을 보자.

Ax가 b의 C(A) 위로의 정사영일 때 Ax와 b의 차이가 최소가 된다. 그림과 매칭시켜 보라.
즉, 최소제곱해는 b를 행렬 A의 column space로 투영시켜 최적의 해를 구한다.
생각해 보면 맞는 말이다.
벡터 위의 그림에서 보이듯 Ax = bc의 해가 Ax = b의 최소제곱해가 되는데
수학적으로는 "x0가 Ax=b의 최소제곱해면 x0는 normal equation의 해가 된다 (역도 성립)"라는 것을 누군가가 증명했기 때문에
우리는 아래와 같은 Ax의 normal equation을 풀면 되는 것이다.

대수적 해석
|| B - AX ||^2를 최소로 하는 X를 찾는 문제
X에 대해 편미분 하고 0이 되는 지점을 찾아보면 결국 AX = B 인 지점을 찾는 문제가 된다.


Linearization of Non-linear Relationships (비선형의 선형화)

이와 같이 최소자승법을 직접적으로 적용해 특정 함수에 피팅하는 것은 모델 파라미터 a, b,... 에 대해 1차 선형이기 때문에 가능하다.
n차 다항 함수는 그 자체로는 선형이 아니지만, 모델 파라미터에 대해서는 선형이 될 수 있다.
1차 이상의 고차 다항식에는 polynomial regression을 이용해 모델 파라미터에 대한 선형식으로 만들고 같은 방식으로 해결한다.
처음 선형 최소다항 문제를 풀 때 2차 함수를 모델로 하는 예시를 들 수 있었던 이유이다.
다항 함수가 아닌 다른 관계도 모델 파라미터에 대해 선형화시킬 수 있을까?
위의 A의 조건, y의 조건을 만족시키는 Ap = y의 형태로 만들 수 있을까?

선형화시킬 수 있는 예제들은 위와 같다. 이상욱 교수님의 유튜브를 참고하기를 추천한다.
모델 파라미터를 선형으로 만들 수 없다면?
원을 모델 함수로 할 때를 예로 들어보자.
원의 방정식은 (x-a)^2 + (y-b)^2 = r^2 이고
전개해서 좌변으로 정리해 보면 x^2-2ax+a^2 + y^2-2by+b^2 - r^2 = 0 이 된다.
우리는 갖고 있는 점의 좌표들로 residual이 최소가 되는 최적의 원의 방정식을 구하고 싶은데, 원의 방정식으로 피팅을 할 때에는 모델 파라미터 (a, b, r)에 대해 1차 선형이 유지되지 않기 때문에 위와 같은 방법을 사용할 수 없다. (문제를 행렬식으로 표현할 수도 없다.)
물론 c를 a^2+b^2-r^2라 잡고 x^2+y^2를 우변으로 넘긴 후에 행렬식 세우고 푼 뒤에 r을 sqrt(a^2+b^2-c)로 구할 수 있지만, 이는 기하학적 해석이 명확하지 않은, 약간 편법적인 방법이며, 보다 정확한 근사를 위해서는 비선형 최소자승법으로 해결해야 한다고 다크프로그래머님께서 정리해 주셨다. (하단에 모든 참고 링크 있음)
따라서 우리는 이러한 비선형 최적화를 풀기 위해 해를 점진적으로 찾는 방법을 이용한다.
비선형 최소자승 문제 : closed-form solution X --> 점진적으로 해를 찾는 방법 (iterative minimization)
다음 글에서 비선형 최소자승을 문제를 푸는 데에 고려해 볼 수 있는 4가지 iterative minimization 기법에 대해 알아보겠다.
1. Gradient Decent Algorithm
2. Newton Method
3. Gauss-Newton Method
4. Levenberg-Marquardt Algorithm
References
아래 글과 영상들이 진짜 정리가 잘되어있어서 도움을 많이 받았다. 특히 다크프로그래머님 블로그 최고 ㅠ_ㅠ
개똥 같은 내 글 말고, 아래 references 참고하는 것 추천드린다...
나도 조금 더 완성도 있는 글을 쓰고 싶어서 미루고 미루다가 그냥 올린다... 새롭게 이해하는 부분이 생기거나 여유가 생기면 틈틈이 업데이트 하겠다. 틀린 부분이나 이해가 부족한 부분에 대해서 지적해 주시면 감사히 배우겠습니다, 여러분!
- https://darkpgmr.tistory.com/56
- https://darkpgmr.tistory.com/132
- https://darkpgmr.tistory.com/142
- 최소제곱법과 다항식 근사
- 정사영 행렬과 QR 분해
- 선형대수학 투영과 최소자승법
- Least Squares Fitting
- 선형 독립
- 데이터 사이언스 스쿨 선형 연립방정식과 역행렬
'스터디 로그 > Internships' 카테고리의 다른 글
| [Project 1] 신호 데이터의 Contact & Release 지점 찾기 (2) (0) | 2023.03.18 |
|---|---|
| 0316 (0) | 2023.03.17 |
| [Project 1] 신호 데이터의 Contact & Release 지점 찾기 (1) (0) | 2023.02.26 |
| 스타일러스 펜 (+ 기술의 종류) (1) | 2023.02.12 |
| 전기용량, 접지, 유도계수, 축전기 (0) | 2023.01.28 |